略谈结构力学

    
    结构力学的任务是什么呢？简单说就是要设计的结构既安全又经济。就这么一句话，却是很费理解的，而且人类经过了几百年的努力，又需要方方面面的合作才能够完满地达到。

 

    首先，一个结构要承担它的使用功能，例如建筑在南方沿海的一座楼房，它不仅要承受日常的载荷，如在楼内生活的人群、各种家具和附属物对楼产生的载荷，楼还要经受台风的考验。建在地震区的结构又要经受地震的考验。结构设计者就要借助结构力学，使设计的结构在以上各种使用的条件下，结构不会丧失它的功能，即使在极端不利的条件下，结构可以开裂或受损，楼房中的人也应当是安全的。一句话，所谓安全，就是要保证结构有足够的强度、刚度和稳定性。从另一方面说，如果为了安全，把结构做得特别结实，多用材料用好材料，楼房多配钢筋做成一个铁疙瘩行不行呢？那样又太浪费了。结构力学就是要帮助设计者掌握一个度，既要安全又要经济。所以结构力学，实在是现代结构设计最重要的手段。

 

    结构力学是怎样做到这一点的呢？从广义的结构力学来说，它需要解决以下三方面的问题：

 

    1、确定结构所受的外力（包括外力、外部热、电磁场等条件）；

 

    2、根据外力和结构的材料性质分析结构内部每一点的应力应变状态和位移；

 

    3、根据得到的应力状态和位移判断结构在所给定的条件下判定结构会不会破坏。

 

    这三个方面的问题，一直是有关结构研究的主要方面，由于问题的复杂性，即使到现在，也不能说都研究清楚了。

 

    对于第一方面的问题，要确定作用在结构上的外力，是很复杂的任务，对于作用在结构上的静力，像结构的自重、加载在结构上的负重（如桥梁上的车辆等）是比较容易弄清楚的，但是作用在结构上的风载、雪载、地震载荷等就不容易弄清楚了，它不仅与风力和震级的大小有关，还和结构所在的地区有关，盖在海南岛与盖在北京的房屋结构，应当考虑的风载就不应当一样。所以就与该地区长期对风速和地震的记录资料是紧密有关的，从这些资料经过专门的分析得到一个该地区设计时应当考虑风力和地震的震级，进入设计规范。类似地，车辆在不平路段行进的颠簸所形成的载荷、船舶在波浪起伏的海上所受的载荷、飞机在航线上由于气流的不稳定所应当考虑的载荷，这些都是要经过大量的资料和实测才能确定下来的。这些资料，也是一个国家设计水平的一项基本建设。
 

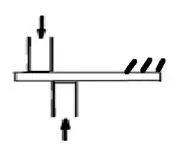
图1 受剪切的钢棒
 

    对于第三方面的研究，即关于材料强度方面的研究，有很长的历史。1638年，伽利略在他的《关于两门新科学的对话》中，就讨论了材料在受拉伸时的强度问题。后来人们发现材料不仅能够拉断，还会被剪断，如图1，上下两个冲头作用下，中间的钢棒会被剪断，而钢棒并没有被拉伸。所以材料的断裂强度问题是足够复杂的。后来人们总结出对于均匀材料根据应力或应变状态的强度判据，不过这还是不能满足需要。随着材料的种类增加，不同材料有不同的强度特点，例如混凝土受压强度很高而受拉的强度又很低，还有各向异性材料，例如木材对于不同方向受拉强度差别很大。进而，材料在不同温度下强度的表现不同，材料在载荷作用下经受的时间长度会影响强度，材料在交变应力作用下的强度，即材料的疲劳强度和损伤的问题都是工程实际中经常遇到的问题。所以材料强度问题，即使到今天，仍然是一个需投入力量研究的方向。

 

    现在我来着重谈谈结构力学第二方面的问题，即根据外力和结构的材料性质分析结构内部每一点的应力应变状态和位移。从根本上来说，结构能够安全，首先是把结构内的应力应变和位移分析得准确，因之这个环节又称为结构分析。从狭义的观点来看，人们经常说的结构力学，主要就指的是结构分析。从历史发展上来看，从狭义的意义上来看，所谓结构力学主要是指杆件系统的应力应变和变形的分析。这是因为，这部知识分形成得比较早，它是结构力学最早系统化的知识。我们现在就着重来谈谈关于杆系的结构力学问题。这是因为关于板壳弹性力学，后来都形成专门的学科。

 

    杆系结构力学的发展是分两步走的：

 

    第一步首先是对一根杆件的力学分析，也就是对于梁的弯曲和杆的拉伸扭转问题的解决；

 

    第二步才是考虑许多杆组合在一起的结构系统的分析问题。

 

    杆的压缩和拉伸的受力问题相对简单，早在1638年，在伽利略的巨著《关于两门新科学的对话》中，就已经大致解决了。所以说是大致解决，是在直杆在受轴向压力或拉力的条件下，杆的内力能够准确地求得，然后用截面大小去除，得到的是单位截面所受的拉压力，用来表征材料的受拉压的强度。至于这时产生的变形，那要等到1678年英国人胡克提出物体的弹性之后才逐渐弄清楚的。

    说到等截面直梁的弯曲问题，那的确是经过了相当长的时期才搞清楚。即使把1638年伽利略在他的《关于两门新科学的对话中》作为精确研究梁的弯曲的研究的开始，直到1826年，法国学者纳维（Louis Henri Navier ，1785 –1836）在他的《力学在结构和机械方面的应用》一书的出版，才算是最后完成，经过了近200年的漫长岁月。这期间，有许多学者对梁进行了研究，其中最重要的是雅各布·伯努利（JacobBernoulli，1654-1765）于1705年发表的论文《弹性梁的弯曲》提出了平截面假定，即梁在变形时梁的横截面保持平面，由此，梁的控制方程大大简化，不过由于他们在求解的过程中，对梁的中性轴（即梁在变形时截面上没有拉压的那点所形成的轴）的位置设定的不正确，所以还是不能得到正确的结果。中性轴的问题由纳维最后解决了，他严格论证，在纯弯曲条件下，梁的中性轴的位置应当是截面的形心。在结构力学中纳维最早提出了超静定结构的概念，并且给出了求解的方法，也就是说这类问题单靠平衡方程不能得到结构内力的全部解，需要加入结构的变形求解，例如图2左那样多根杆的系统与右边的一端固定一端简支的梁就是这样的系统。
 

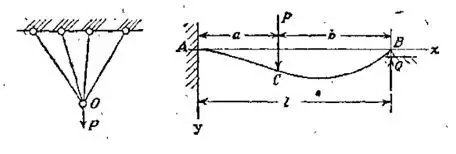
图3 纳维讨论的超静定结构
 

    在他的《力学在结构和机械方面的应用》这本书中，还讨论了挡土墙、桁架、栱、板等结构问题。可以毫不夸张地说纳维的这本书是结构力学中第一本比较全面阐述结构力学的专著，它标志着结构力学成为独立的学科分支。

 

    19世纪50年代，由于炼钢技术的普及，用钢铁作为结构随之也得到普及。钢结构比起用木材和砖石的结构要复杂许多，也轻巧许多，于是就要求结构力学适应新的复杂性的要求。要求更简单易于掌握、适应于分析大量构件组合的结构系统的结构分析方法。适应这样的要求，德国工程师卡尔·库尔曼（Karl Culmann，1821 –1881）于1851年之后将他扩张了的桁架理论进一步发展，用图解的方式去求解，后来称为图解静力学。再后来，曾经在高等学校教学的一些学者：德国物理学家麦克斯韦（James Clerk Maxwell，1831-1879）、德国工程师文科勒（Emil Winkler，1835-1888）、德国工程师莫尔（Christian Otto Mohr，1835-1918）、意大利学者卡斯提也努（Alberto Castigliano，1847-1884）、德国工程师穆勒（Heinrich FranzBernhard Müller，1851-1925）、俄罗斯工程师科皮切夫（Viktor Lvovich Kirpichev，1845-1913）系统地发展了求解超静定结构的方法，这就是后来所称为的力法，他们还发展了图解力学，发展了强度理论。用形变法求解超静定刚架结构是由丹麦的工程师本笛克森（AxelBendixen）在1914年给出的。同时，德国物理学家基尔霍夫（Gustav Robert Kirchhoff，1824-1887）完成了弹性薄板的理论，英国学者乐甫（Augustus Edward Hough Love，1863-1940）完成了弹性薄壳的理论。所有这些发展成为现代结构力学的庞大的体系。这些基本上是在19世纪后半叶和二十世纪前半叶形成的。

 

    二十世纪五十年代电子计算机来到世界上，计算机最早的大规模应用就是用来解决力学问题。随后到六十年代，不仅原先的杆系结构力学问题能够用计算机求解，随着有限单元法的发展，原来办法不多的弹性力学和连续体的力学问题也能够用计算机求解。

 

    随后大量的用计算机求解结构的计算机软件出现，并得到迅速发展，包含二维元、三维元、梁单元、杆单元、板单元、壳单元、流体单元等多种单元、能解决弹性、塑性、流变、流体以及温度场、电磁场各种复杂耦合问题的软件以及软件系统不断出现。在10多年内生产与销售有限元软件形成了有相当规模的社会新产业，而且使用有限元法解决实际问题迅速在工程技术部门普及。1960年克劳夫在匹兹堡举行的美国土木学会电子计算会议上的《平面应力分析中的有限元法》是最早提到有限元的论文。之后有限元的论文、文集、专著大量涌现，专题学术会议不断召开。新的单元、新的求解器不断提出，先后有等参元、高次元、不协调元、拟协调元、杂交元、样条元、边界元、罚单元等不同的单元，有带宽与变带宽消去法、超矩阵法、波前法、子结构法、子空间迭代法等求解方法，还有网格自动剖分等前后处理的研究，这些工作大大加强了有限元法的解题能力，使整架飞机、整条船这样的复杂结构能够一次进行应力和变形分析，使有限元方法逐渐趋于成熟。

 

    结构力学尽管有了空前的发展，不过对于许多非线性结构力学问题，人们的办法还不够多，还有待进行研究。要达到对结构认识的完全自由人们还需要准备走很长的路。

 

    参考文献

 

    [1] Karl-Eugen Kurrer，TheHistory of the Theory of the Structures—— From ArchAnalysis to Computational Mechanics，Ernst & Sohn awiley company，2008.

 

    [2] 武际可，力学史杂谈，结构力学的回顾与发展，高等教育出版社，2009.